Sockeye Code Walkthrough
This document describes how Sockeye implements the Transformer model. It begins with data preparation, then moves into training, and finally decoding. At the heart of Sockeye is a generic structure that implements all three major architectures in neural machine translation: the RNN, the Transformer, and the Convolutional approach.
The document is split into three major sections:
- Data Preparation: raw iterators—prepared iterators—generic interface—terminology—summary
- Training: skeleton—modules—the transformer—encoder—decoder [incomplete]
- Inference [incomplete]
Like most NMT systems, Sockeye’s codebase changes daily. I will be baseing this tutorial on Sockeye v1.18.54 (commit 985c97edecaa93c3ab45e0b93b7a6493a1c5d7c7); all links to the code will be within this branch.
Data Preparation
The basic operation of the training algorithm is to consume sentences of the training data and run forward and backward operations over the computation graph. Sockeye can process this training data in two ways: a traditional way in which the trainer works directly with raw text, or an efficient manner that requires a separate pre-preparation step to organize the raw data into training shards. Both of these approaches are abstracted away beneath Sockeye’s data iterators interface. This API returns DataBatch objects that are fed into training; what varies is which of these two data preparation approaches the user chooses.
It is important to understand basics of how training works. During training, sentences are batched together, meaning that the losses and gradients are computed for many sentences at the same time. Because they are done in parallel, the computation runs to the length of the longest item in the batch. For this reason, NMT attempts to group together sentences of similar lengths into buckets. The buckets are keyed by a tuple (M, N) indicating the length of the maximum source and target sentence lengths. These buckets can be defined in any way the user chooses.
This section will begin with the raw data approach. It is the most intuitive, and its discussion will bring to light issues that arise in training neural machine translation systems. This will motivate the use of prepared data iterators.
Raw data iterators
This “traditional” approach to data iterators makes two passes over the raw data.
It is engaged by passing --source and --target to sockeye.train.
During the first pass, it builds statistics and calculates information about what the batches will look like.
In the second, it assigns data to batches.
It then creates an iterator that iterates over them.
The entry point is get_training_data_iters() in data_io.py.
The steps are laid out fairly clearly:
-
Calculate length ratio (analyze_sequence_lengths). This is a linear pass over the data. After running it, Sockeye knows the number of valid training sentences as well as statistics (mean and standard deviation) of their length ratios.
-
Define the parallel buckets (define_parallel_buckets). A bucket is a pair of integers determining the maximum length (source and target) of a sentence pair in the training data. Sockeye uses
--bucket-width(call it B) to iterate over the target data in steps (B, 2B, 3B, …), defining the lengths of the target bucket, up to--max-seq-len. It then uses the ratio computed above to determine the relative size of the source bucket. At training time, a sentence pair is fit into the smallest bucket that can fit both sides. -
Compute statistics (get_data_statistics). With the buckets defined, Sockeye takes another pass over the training data and computes statistics using a DataStatisticsAccumulator. Afterwards, it knows how many data points (sentence pairs) belong in each bucket, among other things.
-
Define batch sizes. (define_bucket_batch_sizes). Two types of batching are available via
--batch-type: word and sentence based. When using sentence-based batching, all batches have the same number of sentences (and thus batches with shorter sentences take up less memory, since the graph doesn’t need to be rolled out as far). With word-based batching, batches with shorter sentences can fit more of them. After this function returns, we know the batch sizes for each bucket. -
Load data (RawParallelDatasetLoader.load) and ParallelDataSet.fill_up. Finally, the data is loaded into memory with a third pass over the training data. The raw data iterators load the entire training corpus into memory. For each bucket, we know exactly how many data points there are, so we can directly initialize an MXNet NDArray object (though actually, we use numpy first, and then initialize MXNet at the end). As each data point is read in, it is padded with
constants.PAD_ID(i.e., 0) so that it reaches the length of the bucket its in.The complete set of data is returned as a ParallelDataSet. This data all resides in main (i.e., not GPU) memory. There is one small remaining issue. The number of samples for each bucket (i.e., the number of sentences in the training data that fell into, say, bucket (29, 30)) is unlikely to be a multiple of the batch size. In order to have full batches, the remainder must be row-padded, i.e., adding dummy sentences so that the final batch is the correct size. This is accomplished by a call to
fill_up(). -
Create iterator. Sockeye returns a ParallelSampleIter. This is a custom iterator whose ultimate job is to return mx.io.DataBatch objects at each call to
next(). It also supports shuffling both the batches and the data within each batch.
Prepared data iterators
There are a number of problems with the raw data iterators:
- They require the entire training data to be loaded into memory.
- They waste a lot of time at training startup—time when the GPU(s) are not being used.
These problems are exacerbated by the fact that many experiments will make use of the exact same prepared data.
Because of this, Sockeye provides a second, more efficient way to iterate over the training data.
This approach essentially offloads the above training data preparation steps to a separate program (sockeye.prepare_data), which divides the data into shards and then applies the above process to each shard.
Prepared data then defines a new iterator, which traverses all the data in each shard, one at a time.
With this:
- Memory use is at most the size of the largest shard (default: 1m data points).
- There is almost no startup cost, apart from directly loading the first shard into memory.
Preparing the training data
Preparing the training data is accomplished by calling
python3 sockeye.prepare_data --source ... --target ... [--shared-vocab] [other args]
The CLI just wraps a call to data_io.prepare_data(). This functions proceeds along the following steps:
-
As before, it iterates over the training data to collect the mean ratio statistics, and then uses that information to define the bucket sizes.
-
As a second step, the data is randomly assigned to shards. By default, each shard has 1,000,000 data points (sentence pair), though this can be overridden with
--num-samples-per-shard. These shards are plain text. -
Finally, each shard is read and processed to raw mx.nd.NDArray objects, which makes them quite ffast to load at runtime. This is accomplished by using RawParallelDatasetLoader.load() as before. These datasets are then immediate dumped to disk using mx.nd.save, which simply concatenates the source, target, and label streams.
Using prepared iterators
Prepared data iterators are activated in Sockeye via the --prepared-data to sockeye.train.
(This flag is incompatible with --source ... --target ....)
Shards are accessed via the ShardedParallelSampleIter, which is effectively just a shard-aware wrapper around the earlier-described ParallelSampleIter.
In addition to shuffling batches, it shuffles shards.
At each epoch, reset is called, which shuffles everything.
The order of shards is randomized, as is the data within a shard.
However, all the data within each shard is processed before the next shard is loaded.
Data loading is much faster, because (a) the shards are much smaller and (b) each shard has already been written to serialized integer-based NDArray objects (via the vocabulary), and therefore doesn’t have to be constructed.
A generic interface
Sockeye brings this together into a generic API.
In train.py, the function create_data_iters_and_vocabs uses Sockeye’s training parameters to figure out the correct thing to do, hiding the complexity of:
- Choose raw or prepared data iterators
- Starting training or continuing training from an earlier aborted run
Terminology
Here is some of the terminology used in the previous section. Most of this is generic NMT terminology and not specific to Sockeye.
-
Buckets group together sentences in some fashion, usually ones of similar length. Buckets are determined by using increments of
--bucket-widthon the target side, with the source sides computed using the empirical source/target sentence mean ratio. -
A batch takes a group of sentences and runs training over them in parallel. Batches operate on a subset of a bucket; the whole bucket probably doesn’t fit fit, since buckets are usually much larger than batches. Batching can be either sentence-based (with a fixed number of sentences per batch) or word based, which fixes the number of words per batch and determines the number of sentences via sentence length. Word-based batching makes sense since more sentences can be in the batch when they are shorter.
-
A shard is a random subset of the entire training data. By default, a shard contains a million sentence pairs, but this can be changed with the
--num-samples-per-shardflag tosockeye.prepare_data.
Summary
The following table compares training using raw iterators and prepared iterators.
| raw iterators | prepared iterators | |
|---|---|---|
| Entry point | get_training_data_iters() |
get_prepared_data_iters() |
| Iterator | ParallelSampleIter |
ShardedParallelSampleIter |
| Memory | Loads all training data into memory | Shard-by-shard |
| Training time cost | three passes | constant |
Training
The basic function of Sockeye’s training module is to construct a symbolic computation graph and to run data through it.
The assembly of the graph is separated from the execution of the graph, which does not occur until a batch of input examples is passed in via a call to a module’s forward() method.
These concepts will be familiar to you if you have used MXNet or another deep learning toolkit.
In order to make them concrete in MXNet, however, the following steps are the important ones:
- The graph is assembled by linking together various mxnet.sym.Symbols into a computation graph and creating a module.
- The module is placed into GPU memory when module.bind() is called. This call provides the module with the input shapes, from which it can infer all shapes (and required memory usage) throughout the graph.
- The graph is executed when a call to [module.forward()] is made.
Of course, there are many other pieces required to run training. The data preparation section above is one important piece of it. Sockeye contains implementations of all three major NMT architectures, and there are a host of parameters affecting each of them, as well as architecture-agnostic values such as the optimizer to use or the learning rate.
The skeleton
It is often difficult to determine what the most important aspect of an entity is: its essential core, its quiddity.
For example, what is the central or most important part of an automobile?
Well, it couldn’t go anywhere without an engine, so that is certainly a candidate.
But then, it couldn’t go anywhere with wheels, either, or for that matter, seats to hold the driver, who serves the core function of directing the vehicle (since driverless cars are a pipe dream).
Anyone who has spent time around pot smokers may be familiar with arguments of this nature and their notorious circularity and unresolvability.
I have no problem, however, in identifying the golden core of Sockeye, its white-hot center, the engine that drives the entire codebase, its most important and essential piece.
And since there are no MT researchers smoking pot nearby to argue with me, I can even proceed directly to identifying the exact line number without fear of contradiction.
It is lines 107–146 of training.py, in the TrainingModel initialization, where the symbolic graph for a particular sentence pair length is lazily defined, to be later passed to the BucketingModule, which will unroll it on demand.
The function is short enough that it’s worth repeating here:
def sym_gen(seq_lens):
"""
Returns a (grouped) loss symbol given source & target input lengths.
Also returns data and label names for the BucketingModule.
"""
source_seq_len, target_seq_len = seq_lens
# source embedding
(source_embed,
source_embed_length,
source_embed_seq_len) = self.embedding_source.encode(source, source_length, source_seq_len)
# target embedding
(target_embed,
target_embed_length,
target_embed_seq_len) = self.embedding_target.encode(target, target_length, target_seq_len)
# encoder
# source_encoded: (batch_size, source_encoded_length, encoder_depth)
(source_encoded,
source_encoded_length,
source_encoded_seq_len) = self.encoder.encode(source_embed,
source_embed_length,
source_embed_seq_len)
# decoder
# target_decoded: (batch-size, target_len, decoder_depth)
target_decoded = self.decoder.decode_sequence(source_encoded, source_encoded_length, source_encoded_seq_len,
target_embed, target_embed_length, target_embed_seq_len)
# target_decoded: (batch_size * target_seq_len, decoder_depth)
target_decoded = mx.sym.reshape(data=target_decoded, shape=(-3, 0))
# output layer
# logits: (batch_size * target_seq_len, target_vocab_size)
logits = self.output_layer(target_decoded)
loss_output = self.model_loss.get_loss(logits, labels)
return mx.sym.Group(loss_output), data_names, label_names
It is not included in the comments, but this code is the high-level skeleton which manages training for all three architectures in Sockeye. There are five pieces or layers:
- The embedding layer, which computes the source and target word embeddings.
- The encoder layer, which encodes the source sentence, producing a sequence of encoder hidden states.
- The decoder layer, which runs the decoder to produce a sequence of target hidden states.
- The output layer, which produces, for each target word position, a distribution over the target language vocabulary (in the form of raw logits).
- The loss computation, which computes the loss of the output distributions relative against the target labels (the correct answers).
This has been a fairly generic view of how training works. Having defined this central piece, I will work both outward and inward to explain Sockeye’s internals in grounded detail. The “outward” explanation will describe how we get here, that is, the code-specific role this code plays in the construction of the graph, and how it is executed with data fed into the training module. Some of this will be a review of information from the previous section on data preparation.
I will follow that with an “inward” explanation. Three of these skeletal pieces(embedding, the output layer, and loss computation) are shared among all three of Sockeye’s auto-regressive NMT architectures: the RNN, the Transformer, and the convolutional model. The architectures differ in how they construct the encoder and decoder layers. I will explain below how one particular instantiation of this generic skeleton—the Transformer—proceeds with training a model. Along the way you will learn lots of intricacies and secrets of both Sockeye and MXNet.
Modules
Sockeye relies on MXNet’s modules, which implement and execute programs defined by a computation graph, which are built from operations on MXNet Symbols, such as the sym_gen() function above.
They have already come up a number of times.
But while the basic idea is simple, in my opinion, this clarity is muddied a bit by the particulars, so it is worthwhile going over once again.
Modules have a few basic functions:
- Receiving a computation graph definition, in the form of a
Symbol; - initializing or loading parameters for the computation graph;
- executing the graph with actual data.
An important concept in training neural systems is bucketing. This is the process by which similar-sized inputs are grouped together and executed as a batch. MXNet provides some support for bucketing, by allowing the user to provide a function which generates the symbolic graph for a bucket on the fly. This function is keyed to a bucket key, which is a (source length, target length) pair: whenever the bucketing module gets a group of data under a certain bucket key, it generates that graph, caching the result.
When run, the sym_gen() function generates a symbolic graph.
The graph is not actually executed at this point.
The function is defined, but not called.
Even when it is called, the graph is only created, but cannot even be laid out in memory.
That doesn’t occur until the data is passed to MXNet’s “bucketing module” system, which rolls out the graph to different lengths on demand, sharing parameters between them while saving time and computation by allowing buckets with shorter sentences to quit training earlier.
This module is defined a few lines later, where we see.
self.module = mx.mod.BucketingModule(sym_gen=sym_gen,
logger=logger,
default_bucket_key=default_bucket_key,
context=self.context,
...)
Sockeye’s default behavior is to use buckets, but you can turn that off by passing --no-bucketing to sockeye.train (and sockeye.prepare_data, if you are using data preparation).
In that case, Sockeye runs the following code instead:
symbol, _, __ = sym_gen(default_bucket_key)
self.module = mx.mod.Module(symbol=symbol,
data_names=data_names,
label_names=label_names,
logger=logger,
context=self.context,
compression_params=self._gradient_compression_params,
fixed_param_names=fixed_param_names)
Here, you can see how the sym_gen() function is called with the default bucket key.
Since the bucket keys are pairs of (source, target) lengths, the default is to roll out to the longest possible length.
So when bucketing is turned off, Sockeye creates a single graph, and every training instance gets executed all the way to the end.
The bucketing module doesn’t run sym_gen() now, but later, on demand, as it encounters particularly bucket keys (e.g., (30, 27) for a bucket with a maximum source length of 30 and a maximum target length of 27).
The bucketing is basically just a hash function, mapping the bucket keys to unrolled computation graphs.
Each time a new batch is put in, the bucketing module creates the graph if it is not already present.
The graph is created by calling sym_gen().
(The default bucket key is used as the maximum length, and the context is the CPU or GPU(s)).
This is similar to the following design pattern which you have probably written yourself:
def get_dictionary_value(self, key):
if not self.dict.has_key(key):
self.dict[key] = 0
return self.dict[key]
A few lines after module creation, the module is allocated in memory on the specified device (e.g., a GPU).
(Sockeye defaults to looking for a GPU, unless you specify --use-cpu to training or inference).
self.module.bind(data_shapes=provide_data,
label_shapes=provide_label,
for_training=True,
force_rebind=True,
grad_req='write')
Here, the data and label shapes are provided, which allows the computation graph to figure out how much memory it needs.
The computation graph is executed later, in the training.fit() function, where the data iterators from the previous section are iterated over (MXNet actually provides its own fit() implementation, but Sockeye uses its own, in order to have more control over stopping conditions and epochs).
In train.py, Sockeye creates a training data iterator.
This object iterates over the training data, returning a mx.io.DataBatch at each call to next() from the EarlyStoppingTrainer:
def fit(...):
[snip]
while True:
batch = next_data_batch
self._step(self.model, batch, checkpoint_frequency, metric_train, metric_loss)
[snip]
next_data_batch = train_iter.next()
self.model.prepare_batch(next_data_batch)
This batch object is passed directly to TrainingModel.run_forward_backward(), which passes the call to the internal module:
def run_forward_backward(self, batch: mx.io.DataBatch, metric: mx.metric.EvalMetric):
"""
Runs forward/backward pass and updates training metric(s).
"""
self.module.forward_backward(batch)
self.module.update_metric(metric, batch.label)
That’s basically it.
The Transformer
This section introduces you to Sockeye’s implementation of the Transformer model. The goal is not to teach you how the transformer works (there are also a number of good tutorials by Michał Chromiak, Jay Alammar, and Sasha Rush), but how to follow its implementation in Sockeye’s code.
As noted above, with respect to Sockeye’s graph skeleton, the Transformer model is distinct from the other models only in its implementation of the encoder and decoder phases. These implementations are spread across three files: encoder.py, decoder.py, and transformer.py. The first two files are the main ones, with the third containing the TransformerConfiguration as well as support routines used by the encoder or decoder or both.
Transformer Encoder
The top level of the transformer encoder is expressed succinctly in the following code (and below, in Figure 1).
It receives data as input, which is a group of source sentences encoded in a batch.
The batch has a max length (the bucket key), and data_length records the actual length of each sentence in the batch, for masking purposes.
def encode(self,
data: mx.sym.Symbol,
data_length: mx.sym.Symbol,
seq_len: int) -> Tuple[mx.sym.Symbol, mx.sym.Symbol, int]:
"""
Encodes data given sequence lengths of individual examples and maximum sequence length.
:param data: Input data.
:param data_length: Vector with sequence lengths.
:param seq_len: Maximum sequence length.
:return: Encoded versions of input data data, data_length, seq_len.
"""
data = utils.cast_conditionally(data, self.dtype)
if self.config.dropout_prepost > 0.0:
data = mx.sym.Dropout(data=data, p=self.config.dropout_prepost)
# (batch_size * heads, 1, max_length)
bias = mx.sym.expand_dims(transformer.get_variable_length_bias(lengths=data_length,
max_length=seq_len,
num_heads=self.config.attention_heads,
fold_heads=True,
name="%sbias" % self.prefix), axis=1)
bias = utils.cast_conditionally(bias, self.dtype)
for i, layer in enumerate(self.layers):
# (batch_size, seq_len, config.model_size)
data = layer(data, bias)
data = self.final_process(data=data, prev=None)
data = utils.uncast_conditionally(data, self.dtype)
return data, data_length, seq_len
There are a few small items here. The data is cast to 32-bit floats (effectively a NOOP). Dropout is enabled if requested via an MXNet primitive. Next, the bias is created, with dimenions (batch size * heads, 1, max_length). (This is done because the “self-attention” block works with this dimension, and this way, the bias doesn’t have to be reshaped).
Next, we create and link the layers by iterating over them. Each layer is a TransformerEncoderBlock:
self.layers = [transformer.TransformerEncoderBlock(
config, prefix="%s%d_" % (prefix, i)) for i in range(config.num_layers)]
When data = layer(data, bias) is called, the __call__() method is invoked on each of these layers.
This method builds a new layer and links it up with the layer below it, which is passed in as an argument.
This new layer is then returned for further chaining to arbitrary depths.
The complete implementation is here:
def __call__(self, data: mx.sym.Symbol, bias: mx.sym.Symbol) -> mx.sym.Symbol:
# self-attention
data_self_att = self.self_attention(inputs=self.pre_self_attention(data, None),
bias=bias,
cache=None)
data = self.post_self_attention(data_self_att, data)
# feed-forward
data_ff = self.ff(self.pre_ff(data, None))
data = self.post_ff(data_ff, data)
if self.lhuc:
data = self.lhuc(data)
return data
When executed, this code constructs the symbol graph for a single layer, linking up the following pieces:
- pre self-attention (a TransformerProcessBlock)
- self-attention (layers.MultiHeadSelfAttention)
- post self-attention (another TransformerProcessBlock)
- a pre feed-forward layer (another TransformerProcessBlock)
- a feed-forward layer (a TransformerFeedForward)
- a post feed-forward layer (another TransformerProcessBlock)
- an optional LHUC layer (Vilar, NAACL 2018)
This is visualized in Figure 1 (except for LHUC). The blue boxes denote the dimensions of the tensors that are output from each sub-block (unannotated lines keep the same shape of their inputs). Each block is also labeled with the Sockeye class that processes that block.
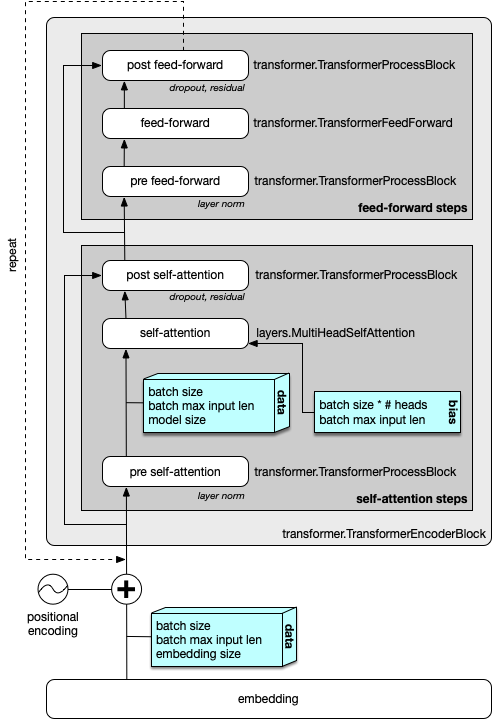
Getting back to the code, these items are all defined in the TransformerEncoderBlock initializer:
self.pre_self_attention = TransformerProcessBlock(sequence=config.preprocess_sequence,
dropout=config.dropout_prepost,
prefix="%satt_self_pre_" % prefix)
self.self_attention = layers.MultiHeadSelfAttention(depth_att=config.model_size,
heads=config.attention_heads,
depth_out=config.model_size,
dropout=config.dropout_attention,
prefix="%satt_self_" % prefix)
self.post_self_attention = TransformerProcessBlock(sequence=config.postprocess_sequence,
dropout=config.dropout_prepost,
prefix="%satt_self_post_" % prefix)
self.pre_ff = TransformerProcessBlock(sequence=config.preprocess_sequence,
dropout=config.dropout_prepost,
prefix="%sff_pre_" % prefix)
self.ff = TransformerFeedForward(num_hidden=config.feed_forward_num_hidden,
num_model=config.model_size,
act_type=config.act_type,
dropout=config.dropout_act,
prefix="%sff_" % prefix)
self.post_ff = TransformerProcessBlock(sequence=config.postprocess_sequence,
dropout=config.dropout_prepost,
prefix="%sff_post_" % prefix)
self.lhuc = None
if config.use_lhuc:
self.lhuc = layers.LHUC(config.model_size, prefix=prefix)
The TransformerProcessBlock appears many times throughout this.
It is a layer which performs pre- and post-processing of data sequences within the transformer.
It applies any subset of layer (n)ormalization, (r)esidual connections, and (d)ropout.
Many of these variables are controlled with the --transformer-preprocess and --transformer-postprocess flags, documented here, which default to ‘n’ and ‘dr’, respectively.
Pulling this all together, we have something that is very similar to the encoder side of Figure 1 in the Transformer paper. Differences from that diagram are:
- Sockeye adds explicit pre-processing blocks before the multi-head self-attention and feed-foward layers
- Sockeye (by default) applies layer normalization before the multi-head attention and feed foward layers, and applies drop-out afterwards; residual connections remain in place.
Multi-headed Self Attention
Most of the layers above are clear enough. However, Multi-head attention, and all its variants—multi-head self attention in the encoder, and multi-head (source) attention and masked multi-head (self) attention in the decoder—benefit from some further explanation. Recall that the goal of attention is to (a) compute a distribution across source words and (b) use this distribution to produced a weighted sum of representations. The first part (a) is computed with a softmax over the comparison of a hidden state against each of the source encodings, and the second part (b) is computed by multiplying this distribution against those same source encodings.
First, a note on terminology, specifically related to Vaswani et al.’s generalization (Section 3.2) of queries, keys, and values. They write:
An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.
This is a nice generalization over the kinds of attention used by the transformer. Writing specifically of multi-head encoder self-attention, it might not be clear from their paper that the queries, keys, and values are all the same thing. For layer \(l\), the queries, keys, and values are all the encoder hidden state at the previous layer. The hidden state representation for each source word is compared to every other word, including itself, to produce a distribution over each words. That distribution is then used to produce a weighted sum of the source representations.
Here we focus just on multi-head self attention, which is the only version that’s used in the decoder.
Self-attention provides two main benefits: (a) direct access to the encoding for any word, and (b) removal of the source-side recurrent computations.
Direct access to encodings is possible because each state is computed as a weighted sum of the states of the layer below it.
(For the first encoder layer, the layer beneath is the positionally-encoded embeddings.)
Contrast this to an RNN, where the encoding for each word is a function of (a) the encoder output for the previous word in the same layer and (b) the encoder output for the same word in the previous layer (again, with the embeddings acting as a 0th layer).
In the RNN setting, for source word i, information about states of words other than i must be filtered through the encoder state mechanism.
This setup attenuates the influence of long-distance dependencies.
The transformer allows the encoder state at each position to look directly at any word in the source.
A consequence of this is that all the encoder states in a layer can be computed simultaneously, which speeds up training.
Sockeye accomplishes this in layers.py in the MultiHeadSelfAttention class.
When the computation graph for the layer is constructed, the following code block (MultiHeadSelfAttention.__call__()) is executed:
# inputs shape (batch, max_length, depth)
combined = mx.sym.FullyConnected(data=inputs,
weight=self.w_i2h,
no_bias=True,
num_hidden=self.depth * 3,
flatten=False,
name="%sqkv_transform" % self.prefix)
# Shape: (batch, max_length, depth)
queries, keys, values = mx.sym.split(data=combined, num_outputs=3, axis=2)
if cache is not None:
# append new keys & values to cache, update the cache
keys = cache['k'] = keys if cache['k'] is None else mx.sym.concat(cache['k'], keys, dim=1)
values = cache['v'] = values if cache['v'] is None else mx.sym.concat(cache['v'], values, dim=1)
return self._attend(queries,
keys,
values,
lengths=input_lengths,
bias=bias)
This takes the input (variable inputs with shape (batch, max_source_len, input_depth)), and projects the entire input through a fully connected layer that triples its size.
(Note that this means that the queries, keys, and values are not passed directly, but instead go first through this feed-forward layer).
Symbol inputs has shape (batch_size, max_length, input_depth) and combined has shape (batch_size, max_length, input_depth * 3).
These projections then become the queries, keys, and values with the call to mx.sym.split().
Next is caching, which I will skip because it is only used by decoder self attention.
The final piece is computing the context vector via a call to _attend() in MultiHeadAttentionBase.
It is defined as follows.
I will walk through it:
def _attend(self,
queries: mx.sym.Symbol,
keys: mx.sym.Symbol,
values: mx.sym.Symbol,
lengths: Optional[mx.sym.Symbol] = None,
bias: Optional[mx.sym.Symbol] = None) -> mx.sym.Symbol:
"""
Returns context vectors of multi-head dot attention.
:param queries: Query tensor. Shape: (batch_size, query_max_length, depth).
:param keys: Keys. Shape: (batch_size, memory_max_length, depth).
:param values: Values. Shape: (batch_size, memory_max_length, depth).
:param lengths: Optional lengths of keys. Shape: (batch_size,).
:param bias: Optional 3d bias.
:return: Context vectors. Shape: (batch_size, query_max_length, output_depth).
"""
The queries are first scaled down by dividing them by the square root of the number of head dimensions:
# scale by sqrt(depth_per_head)
queries = queries * (self.depth_per_head ** -0.5)
Next, split_heads() is called, which reshapes and transforms the input symbol from (batch_size, source length, depth) to (batch * num_heads, source length, model_size / heads).
The multiple heads are just multiple independent attention mechanisms, each computed over the full source, and which are distinguished in training with random initialization.
Below, they will be projected down to a smaller dimension, and all concatenated together, such that the original input dimension, called the “model size”, is restored.
As a result of this downward projection and concatenation, the model size (Sockeye: --transformer-model-size) must be divisible by the number of heads (--transformer-attention-heads).
The defaults are 512 and 8.
The model size must also be equal to the embedding size, since the embeddings serve as their own attention layer for the first layer self attention.
This is done to the queries, the keys, and the values.
# (batch*heads, length, depth/heads)
queries = split_heads(queries, self.depth_per_head, self.heads)
keys = split_heads(keys, self.depth_per_head, self.heads)
values = split_heads(values, self.depth_per_head, self.heads)
The last operation basically multiplied out the first dimension of the tensor to (batch * num_heads). Next, Sockeye broadcasts the lengths of each input sentence in the batch across this flattened axis. Lengths is used in the decoder for masking the attention mechanism so that it cannot see timesteps in the future:
lengths = broadcast_to_heads(lengths, self.heads, ndim=1, fold_heads=True) if lengths is not None else lengths
Finally, we compute dot attention.
This corresponds to Equation 1 in Vaswani et al..
It is itself somewhat involved, but I am not going to go into it because I am tired.
You can read the short function for yourself here.
Basically, it makes use of MXNet primitives (mx.sym.batch_dot, mx.sym.SequenceMask, and mx.sym.softmax) to compute the context vector for each attention head.
# (batch*heads, query_max_length, depth_per_head)
contexts = dot_attention(queries, keys, values,
lengths=lengths, dropout=self.dropout, bias=bias, prefix=self.prefix)
The results of the attention heads are then rearranged to transform shape (batch * heads, source_len, depth_per_head) to (batch, source_len, depth). From that, another feed-forward layer yields the contexsts for the layer.
# (batch, query_max_length, depth)
contexts = combine_heads(contexts, self.depth_per_head, self.heads)
# contexts: (batch, query_max_length, output_depth)
contexts = mx.sym.FullyConnected(data=contexts,
weight=self.w_h2o,
no_bias=True,
num_hidden=self.depth_out,
flatten=False)
return contexts
In this way, the attention mechanisms for all heads, and for all words in the sentence, and all sentences in the batch, are computed in parallel.
Transformer Decoder
The Transformer decoder is a lot like the Transformer encoder. There is really only one difference: each decoder layer adds masked self-attention, which, analogous to source-side attention in the encoder, is an attention block over the target side word representations one layer down. Masked self-attention is used because we need to mirror the inference-time scenario where words are generated one-by-one, left-to-right. We therefore need to ensure that the decoder does not attend to words that haven’t been generated yet, which is accomplished by masking out those positions in the fixed-length vector.
Each decoder layer also includes an attention block over the source sentence. The decoder source-attention and self-attention blocks differ in their inputs; masked (target-side) self-attention takes as input the positionally-encoded target-side sequence, and the source attention block returns the output of this block in addition to the top layer of the encoder. This way, the decoder is able to attend both to the source and to the words in the target as they are generated.
Inference
In training, we created (via the bucketing module) a symbolic graph that was “rolled out” to the lengths defined by the bucket key, a tuple containing the maximum source and target length of any sentence in the batch. It was then executed via a single call. This is a nice scenario that we are no longer able to use at inference time, due to the following differences from training:
- We don’t know the length of the target sentence, so we can’t construct a single symbolic graph.
- We don’t know the words of the target sentence, so we don’t have the words needed for decoder self-attention.
Inference in Sockeye and MXNet, therefore, differs from training. We can still compute the embeddings and run the encoder stage for all three architectures, but decoding is quite different. Instead of rolling out the entire decoder graph, we repeatedly construct a decoder graph that is rolled out just a single step. We will then effectively run this single decoding step again and again, each time feeding it the relevant outputs from the previous time step, until some stopping criterion is reached. We will also expand this mechanism to enable beam search.
This section will walk through how Sockeye accomplishes inference. Perhaps surprisingly, a single generic interface is used at inference time, as well, enabling decoding with all three neural architectures. This is possible because they are all auto-regressive in nature.
Build the network
This happens in InferenceModel.initialize(). There is one InferenceModel per “-m” switch from the command line.
- Construct the encoder and decoder modules
- Get the encoder and decoder shapes. Encoder shapes are the same for all models: an mx.io.DataDesc object with C.SOURCE_NAME. The decoder states vary by model and are passed from step to step.
- bind() the module to the shapes [TODO: understand this]
- Initialize the parameters of each of the modules [which can now be read because of the data descriptor that was bound to them?]
Once the models are all loaded, translate.py calls translate(), which in turn calls Translator.translate() in inference.py. Eventually we get to _beam_search().
Run the encoder
Here we call translator._encode(), which calls model.run_encoder() for every model. Each one of these returns a ModelState, which wraps together each model’s decoder states. Each model has only a single encoder output, but many different decoder outputs.
After running the encoder by calling encoder_module.forward(), we get its outputs by calling encoder_module.get_outputs(). We then repeat these states over and over to fill the entire beam, and initialize a ModelState object with them.